作者:ZZR
问题背景
考虑一个问题:现在我们有一些过往核发信用卡的资料,包括用户个人信息和审核结果。根据这些资料,我们希望预测能不能给下一个用户发信用卡。用户基本信息如下:
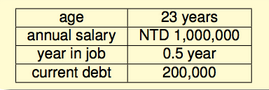
这些基本信息组成了一个向量$X={x_1, x_2, ..., x_d}$。不同的信息有不同的权重,设权重向量$W = {w_1, w_2, ..., w_d}$。我们希望构造一个函数来给用户的信用打分,并且,如果信用分超过了某个阈值,我们就认为这个客户是可靠的,可以给他发信用卡:
- 能发:$\sum_{i=1}^{d}w_ix_i > threshold$
- 不能:$\sum_{i=1}^{d}w_ix_i < threshold$
通过阶跃函数$sign(x)$,进一步将这个过程函数化:
$$y=sign((\sum_{i=1}^{d}w_ix_i)-threhold)$$
所以,当$y=1$,通过;当$y=-1$,拒绝;当$y=0$,忽略。
其中: $sign(x) = \begin{cases} & 1 \quad\text{ if } x>0 \ & 0 \quad\text{ if } x=0 \ & -1\ \text{ if } x<0 \end{cases}$
整理该方程如下:
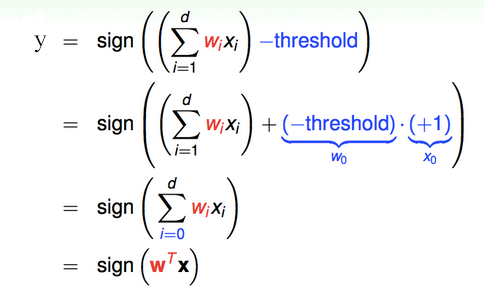
具体到二维空间
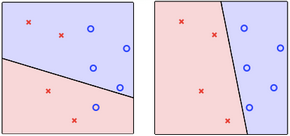
简化上面的问题,假设用户只有两个属性,就可以用二维空间的一个点来表示一个用户。如下所示,蓝圈表示通过,红叉表示拒绝。注意到直线的两边,一边大于0,一边小于0,也就是一边都是蓝圈,一边都是红叉。所以现在的目标就是,找到一条直线$h(x)=w_0+w_1x_1+w_2x_2$,可以将已知的蓝圈和红叉完美区分开。
基础知识回顾
简单回顾一下线性代数的知识。一条直线可以由一个点 $M_0=(x_0, y_0)$和法向量 $\vec{n}=(A, B)$唯一确定。其点法式方程为:$A(x-x_0)+B(y-y_0)=0$。相应地,其方向向量为:$\vec{v}=(B, -A)$
感知机学习算法

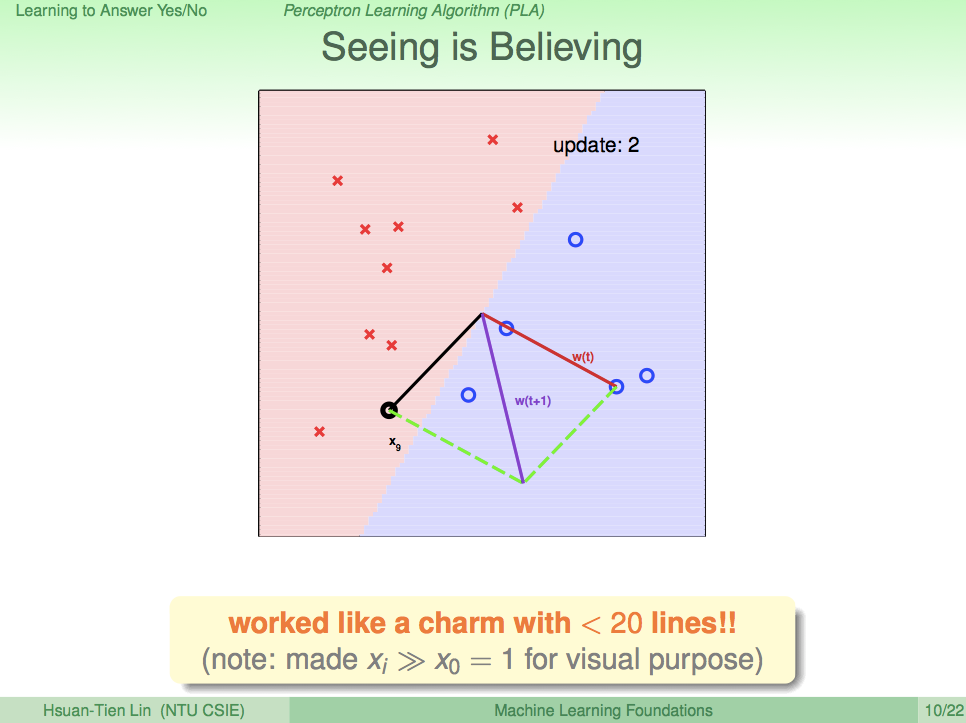
简单感知机算法(Perceptron Learning Algorithm,PLA)的思路很简单,首先随便找一条直线,然后遍历每一个已知点,如果正确,则跳过;如果错误,则利用这个点的信息对直线进行修正。修正的思路如上图所示:$W$是直线$h(x)$的法向量。$X$是错误点的方向向量,$y$是真实值。具体情况可分为如下两种情况:
情况一:$y=+1$
](http://static.zybuluo.com/zzr0427/96htsebxao59sd2fh47dybdo/image_1b2kdgvf21qi2ai91a1v145k14t13f.png)
为了将这个出错的点包括进紫色区域,$W$应该靠近$X$方向。因此,$W(t+1)=W(t)+X$。
情况二:$y=-1$
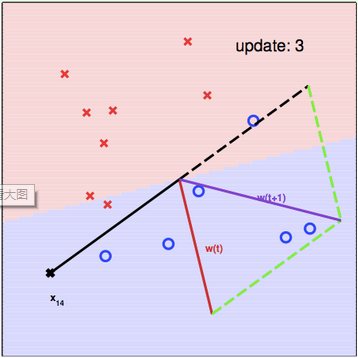
为了将这个出错的点排除出紫色区域,$W$应该远离$X$方向。因此,$W(t+1)=W(t)-X$。
综上,得到修正函数:$$W_{t+1}=W_t+y_nX_n$$
证明:PLA校正的正确性
那么为什么感知机算法可以逐步接近正确呢?
已知$W_{t+1}=W_t+y_nX_n$
两边同时乘上$y_n$和$X_n$,得:$y_nW_{t+1}^TX_n=y_nW_t^TX_n+(y_n)^2X_n^TX_n$
因为$(y_n)^2X_n^TX_n\geq0$,所以:$y_nW_{t+1}^TX_n\geq y_nW_t^TX_n$
注意到$W_t^TX_n$恰好就是我们给出的当前用户的分数。当$y_n>0$,也就是我们打分打低了,修正后分数上升;当$y_n<0$,也就是我们打分打高了,修正后分数下降。这个结论说明,对于$X_n$这组错误数据,经过修正以后,我们打出的分数更靠近正确结果了。
证明:PLA终止的充分条件
从算法的规则上可以看出,PLA终止的必要条件是数据集中确定存在一条直线,可以将蓝圈和红叉分开,也就是线性可分:
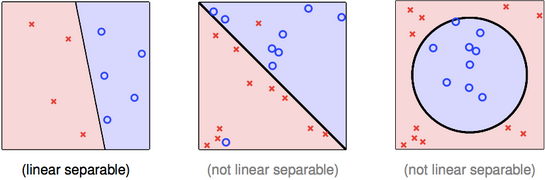
现在证明,线性可分是PLA终止的充分条件。
(1) 设$X_t$表示第$t$次更新时的点,一共更新了n次。若线性可分,则必然存在一条完美的直线$W_f$,使得对$\forall 1\leq t\leq n$,有$y_tW_f^TX_t>0$。也就是: $$y_tW_f^TX_t\geq \min \limits_{1\leq t\leq n}y_tW_f^TX_t>0$$
($W_f\cdot W_t$为向量内积,也就是$W_f^TW_t$)又由$W_t$的更新规则得: $$W_f\cdot W_t=W_f\cdot(W_{t-1}+y_tX_{t-1})=W_f\cdot W_{t-1}+y_tW_f\cdot X_{t-1}\geq W_f\cdot W_{t-1}+\min \limits_{1\leq k\leq n}y_kW_f\cdot X_k$$ 因此: $$\begin{matrix} W_f\cdot W_{t} & \geq & W_f\cdot W_{t-1} & + & \min \limits_{1\leq k\leq n}y_kW_f\cdot X_k\ W_f\cdot W_{t-1} & \geq & W_f\cdot W_{t-2} & + & \min \limits_{1\leq k\leq n}y_kW_f\cdot X_k\ \cdots & & \cdots & & \cdots \ W_f\cdot W_1 & \geq & W_f\cdot W_0 & + & \min \limits_{1\leq k\leq n}y_kW_f\cdot X_k \end{matrix}$$ 综上,得到: $$W_f\cdot W_t\geq W_f\cdot W_0+t\times \min \limits_{1\leq k\leq n}y_kW_f\cdot X_k$$ 初始时$W_0=0$,所以: $$W_f\cdot W_t\geq t\times \min \limits_{1\leq k\leq n}y_kW_f\cdot X_k$$
(2) 因为每次遇到错误的数据才会更新,也就是$sign(W_t^TX_t)\neq y_t$,也就是$y_tW_t^TX_t\leq0$。其中$W_t$是第t次更新时的权重值。因此:
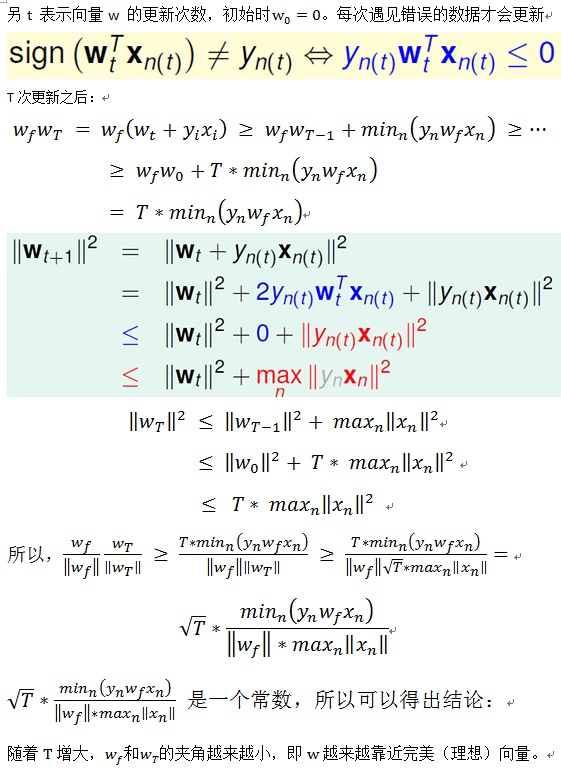](http://static.zybuluo.com/zzr0427/lzd9s0c1z93dkw614gnfkre6/image_1b2kpb26418etikn10r9120ggbl53.png)
类似于(1),得到: $$\left \| W_t \right \|^2\leq t\times\max \limits_{1\leq k\leq n}{\left \| X_k \right \|}^2$$
(3) 综上,得: $$\frac{W_f}{\left \| W_f \right \|}\cdot\frac{W_t}{\left \| W_t \right \|} \geq \frac{t\times \min \limits_{1\leq k\leq n}y_kW_f\cdot X_k}{{\left \| W_f \right \|}{\left \| W_t \right \|}} \geq \frac{t\times \min \limits_{1\leq k\leq n}y_kW_f\cdot X_k}{\left \| W_f \right \|\sqrt{t}\max \limits_{1\leq k\leq n}{\left \| X_k \right \|}} =\sqrt{t}\times\frac{\min \limits_{1\leq k\leq n}y_kW_f\cdot X_k}{\left \| W_f \right \|\times\max \limits_{1\leq k\leq n}{\left \| X_k \right \|}}$$
$A=\frac{\min \limits_{1\leq k\leq n}y_kW_f\cdot X_k}{\left \| W_f \right \|\times\max \limits_{1\leq k\leq n}{\left \| X_k \right \|}}$是一个常数,因此,随着$t$的增大,$\frac{W_f}{\left \| W_f \right \|}\cdot\frac{W_t}{\left \| W_t \right \|}$也逐步增大,也就是向量$W_f$和$W_t$的夹角逐渐减小,$W_t$逐渐接近$W_f$。 又因为:$cos\theta = \frac{W_f}{\left \| W_f \right \|}\cdot\frac{W_t}{\left \| W_t \right \|} \leq 1$,所以$t\leq\frac{1}{A^2}$。因此,PLA算法必然收敛。
Linear Pocket Algorithm
上述PLA算法的前提是数据集线性可分。但是很明显,在分类之前我们不可能知道我们手里的数据是不是线性可分的。更何况,数据集可能有噪声(noise),这些噪声是之前的经验中错误的分类结果,这些噪声将导致PLA无法收敛。因此,我们的目标就从找到一条完美划分数据集的$W_f$,变成了找到一条最接近完美$W_g$,使得错误的点最少。这个转变使得我们可以处理非线性可分的数据集:
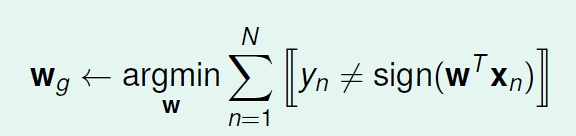 但是很遗憾的是,寻找$W_g$是一个NP-hard问题。
但是很遗憾的是,寻找$W_g$是一个NP-hard问题。
因此问题又从“寻找最接近完美的$W_g$”变成了“寻找尽可能完美的$W_g$”。Pocket Algorithm是PLA的变形,用于处理此类问题。算法如下:

与简单PLA不同的是:
- Pocket Algorithm事先设定迭代次数,而不是等算法自己收敛;
- 随机遍历数据集,而不是循环遍历;
- 遇到错误点校正$W_t$时,只有当新得到的$W_{t+1}$优于$W_t$(也就是错误更少)时才更新$W_t$。因为Pocket要比较错误率,需要计算所有的数据点,因此效率要低于PLA。
- 如果数据集巧合是线性可分的,只要迭代次数够多,Pocket和PLA的效果是一样的,只是速度慢。
实践
讲了这么多理论知识,现在用python实践一下这个算法。简单起见,这里已知数据集是线性可分的,直接采用简单PLA就可以解决。核心代码不到20行,只需要理解train()函数即可,其它部分都是为了把这个图画出来。
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
tmp = np.genfromtxt('linear_separable_train.csv', delimiter=',')
datum = tmp[1:, 1:]
labels = tmp[1:, 0]
history = []
fig = plt.figure()
ax = plt.axes()
x = np.arange(-6, 6, 1)
line, = ax.plot([], [], 'r-', linewidth=2)
label = ax.text([], [], '')
def init():
line.set_data([], [])
for data, label in zip(datum, labels):
if np.sign(label) == 1:
plt.plot(data[0], data[1], 'bo')
else:
plt.plot(data[0], data[1], 'rx')
return line,
def train():
global history
W = np.zeros(3) # [w0, w1, w2]
iter = 0
while True:
iter += 1
mistake = 0
for data, label in zip(datum, labels):
X = np.insert(data, 0, np.array([1])) # [1, x1, x2]
if np.sign(label) != np.sign(np.dot(W, X)):
mistake += 1
W += label * X
history.append(list(W))
if not mistake:
break
return W
def update(i):
global history
w = history[i]
y = (-w[0] - w[1] * x) / w[2]
line.set_data(x, y)
ax.set_xlabel('iter%d' % (i + 1))
print('iter%d wo=%f w1=%f w2=%f' % (i + 1, w[0], w[1], w[2]))
return line,
if __name__ == '__main__':
train()
anim = FuncAnimation(fig, update, init_func=init, frames=len(history), interval=1000)
anim.save('line.gif', fps=1000, dpi=50, writer='imagemagick')
plt.show()
运行效果如下:
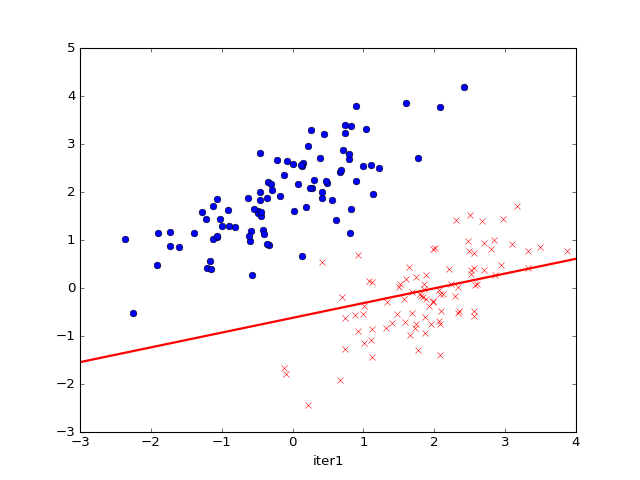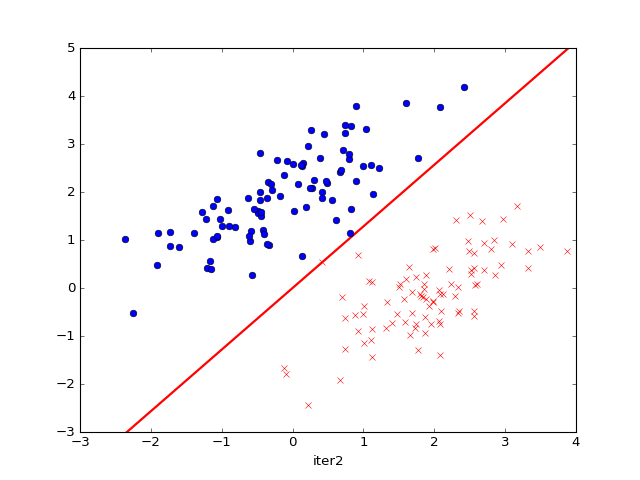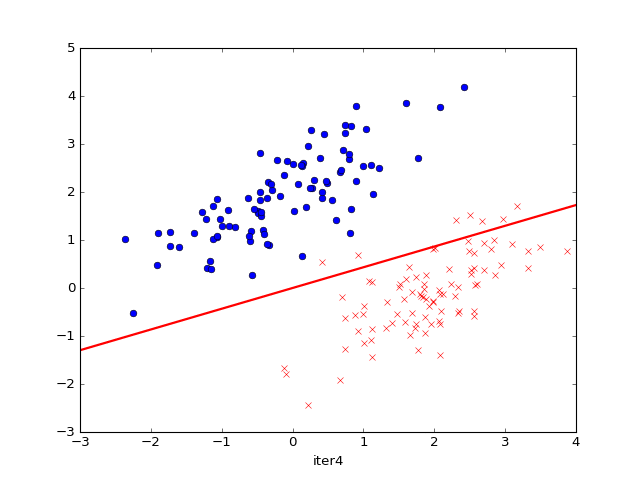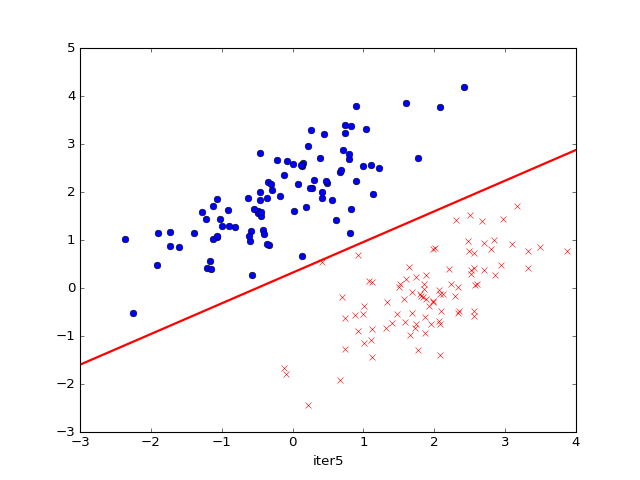
参考资料
- 《台湾大学-机器学习基石-林轩田》第二讲 Perceptron Learning Algorithm
配图来自《台湾大学-机器学习基石-林轩田》
本文内容学习自互联网,采用署名-非商业性使用-相同方式共享 2.5 中国大陆协议进行许可。如需转载,请保留文章所引用的那些原作者的信息。感谢原作者们的精彩分享。如有遗漏的引用,烦请告诉我,我将修改引用或删除文章。